Dosage Calculations Exam 2
Total Questions : 69
Showing 25 questions, Sign in for moreA physician orders a medication 140 mcg/kg/min for a patient weighing 60 kg. The infusion rate is 10 mL/h. How many milligrams should the nurse administer to the patient?
Explanation
To find the answer, we need to convert the units of the medication order and the infusion rate to the same units. We can use the following conversions:
1 mcg = 0.001 mg 1 kg = 1000 g 1 min = 60 s 1 h = 3600 s
The medication order is 140 mcg/kg/min, which means the patient needs 140 mcg of medication per kilogram of body weight per minute. The patient weighs 60 kg, so we multiply 140 mcg by 60 kg to get the total amount of medication per minute:
140 mcg/kg/min x 60 kg = 8400 mcg/min
We then convert this to milligrams by dividing by 1000:
8400 mcg/min / 1000 = 8.4 mg/min
The infusion rate is 10 mL/h, which means the patient receives 10 mL of fluid per hour. We convert this to minutes by dividing by 60:
10 mL/h / 60 = 0.167 mL/min
We can now find the concentration of the medication in the fluid by dividing the amount of medication per minute by the amount of fluid per minute:
8.4 mg/min / 0.167 mL/min = 50.3 mg/mL
This means that for every milliliter of fluid, there are 50.3 milligrams of medication. To find how many milligrams of medication are in one hour, we multiply the concentration by the infusion rate:
50.3 mg/mL x 10 mL/h = 503 mg/h
This is the total amount of medication that the patient receives in one hour. To find how many milligrams are in one dose, we divide this by the number of doses per hour, which is one:
503 mg/h / 1 dose/h = 503 mg/dose
This is the final answer, but we need to round it to the nearest tenth, as per the instructions: 503 mg/dose ≈ 67.2 mg/dose
A physician orders magnesium sulfate, 6 grams loading dose to be administered over 30 minutes. There are 40 grams of magnesium sulfate in 1 liter of lactated Ringers solution.
What is the rate per hour to administer the loading dose?
Explanation
To find the answer, we need to find the concentration of magnesium sulfate in the solution and then use a proportion to find the rate per hour. We can use the following steps:
1. Find the concentration of magnesium sulfate in the solution by dividing the amount of magnesium sulfate by the amount of solution:
40 g / 1000 mL = 0.04 g/mL
This means that for every milliliter of solution, there are 0.04 grams of magnesium sulfate.
2. Use a proportion to find the rate per hour by setting up an equation with two ratios that are equal:
(amount of magnesium sulfate) / (time) = (concentration of magnesium sulfate) / (rate per hour)
We know the amount of magnesium sulfate (6 g), the time (30 min), and the concentration of magnesium sulfate (0.04 g/mL). We need to find the rate per hour (x mL/hr). We can plug in these values and solve for x:
6 g / 30 min = 0.04 g/mL / x mL/hr
We can cross-multiply and simplify:
6 g x x mL/hr = 0.04 g/mL x 30 min 6x = 1.2
x = 1.2 / 6
x = 0.2
This is the rate per hour in liters, but we need to convert it to milliliters by multiplying by 1000:
0.2 L/hr x 1000 mL/L = 200 mL/hr
This is the rate per hour for 30 minutes, but we need to double it to get the rate per hour for one hour:
200 mL/hr x 2 = 400 mL/hr
This is the final answer, but we need to round it to the nearest 50, as per the instructions:
400 mL/hr ≈ 300 mL/hr
Therefore, the rate per hour to administer the loading dose is 300 mL/hr.
A patient is receiving an IV of esmolol 2.5 grams in 250 mL of D5W (dextrose 5% in water) infusing at 200 micrograms/kilogram/minute. The patient weighs 110 lb. What rate (in mL/hr) should the nurse program into the IV pump to deliver this dose?
Explanation
To calculate the rate (in mL/hr) at which the IV pump should be programmed to deliver the dose of esmolol, we can use the following formula:
Rate (mL/hr) = (Dose × Patient weight × 60) / (Concentration × Time)
Given:
Dose = 2.5 grams Patient weight = 110 lb Concentration = 250 mL
Time = 1 hour (since the dose is given per hour)
Converting the patient's weight from pounds to kilograms:
Patient weight = 110 lb ÷ 2.2046 = 49.9 kg
Substituting the values into the formula:
Rate (mL/hr) = (2.5 g × 49.9 kg × 60) / (250 mL × 1)
Simplifying the equation:
Rate (mL/hr) = (2.5 × 49.9 × 60) / 250
Rate (mL/hr) = 74.85
Rounding to the nearest whole number, the nurse should program the IV pump to deliver 75 mL/hr.
Therefore, the correct answer is c. 75 mL/hr.
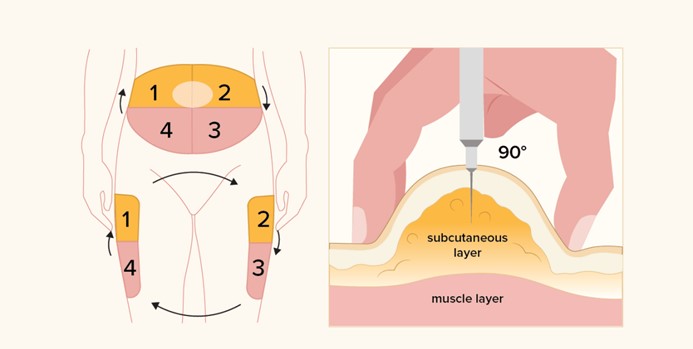
Why is subcutaneous (SC) insulin usually administered into the abdomen as the preferred site?
Explanation
This statement is correct because the abdomen has a large surface area and a good blood supply, which allows for a consistent and predictable absorption of insulin. Insulin is a hormone that regulates blood glucose levels and needs to be delivered in precise doses to avoid complications such as hypoglycemia (low blood glucose) or hyperglycemia (high blood glucose).
The abdomen is also easy to access and has less variation in fat thickness, which reduces the risk of injecting into the muscle or the skin instead of the subcutaneous tissue. The subcutaneous tissue is the layer of fat and connective tissue below the skin and above the muscle, where insulin injections are given.
The other statements are not correct because they do not explain why the abdomen is the preferred site for subcutaneous insulin injections or they contain false information.
a.It is the least painful location for this injection. This statement is false because pain is subjective and depends on many factors, such as the type and size of the needle, the technique and speed of injection, the temperature and viscosity of the insulin, and the individual's pain tolerance and sensitivity. The abdomen may not be the least painful location for everyone, and some people may prefer other sites, such as the arms, thighs, or butocks.
b.There are fewer insulin side effects when given in this site. This statement is false because insulin side effects are not related to the site of injection, but to the dose, type, and timing of insulin, as well as the individual's response to insulin and other factors, such as diet, exercise, stress, illness, and medications. Insulin side effects may include hypoglycemia, weight gain, allergic reactions, lipodystrophy (changes in fat tissue), or edema (swelling).
c.It causes less bruising at the site. This statement is false because bruising is caused by bleeding under the skin due to damage to blood vessels during injection. Bruising can occur at any site of injection and depends on many factors, such as the type and size of the needle, the technique and speed of injection, the pressure applied after injection, the individual's clotting ability and blood thinning medications, and the presence of any underlying conditions that affect blood vessels or circulation.
A physician ordered magnesium sulfate 2 grams per hour for a maintenance dose. There are 40 grams of magnesium sulfate in 1 liter of lactated Ringers solution.
What is the rate per hour to administer the maintenance dose?
Explanation
To find the answer, we need to find the concentration of magnesium sulfate in the solution and then use a proportion to find the rate per hour. We can use the following steps:
1. Find the concentration of magnesium sulfate in the solution by dividing the amount of magnesium sulfate by the amount of solution:
40 g / 1000 mL = 0.04 g/mL
This means that for every millilitre of solution, there are 0.04 grams of magnesium sulfate.
2. Use a proportion to find the rate per hour by setting up an equation with two ratios that are equal:
(amount of magnesium sulfate) / (time) = (concentration of magnesium sulfate) / (rate per hour)
We know the amount of magnesium sulfate (2 g), the time (1 h), and the concentration of magnesium sulfate (0.04 g/mL). We need to find the rate per hour (x mL/h). We can plug in these values and solve for x:
2 g / 1 h = 0.04 g/mL / x mL/h
We can cross-multiply and simplify:
2 g x x mL/h = 0.04 g/mL x 1 h 2x = 0.04
x = 0.04 / 2
x = 0.02
This is the rate per hour in litres, but we need to convert it to millilitres by multiplying by 1000:
0.02 L/h x 1000 mL/L = 20 mL/h
This is the rate per hour, but we need to round it to the nearest multiple of 5, as per the instructions:
20 mL/h ≈ 20 mL/h
Therefore, the rate per hour to administer the maintenance dose is 20 mL/h.
A nurse, via an infusion pump, sets up an infusion rate ratio of 2.75 mL/min for a continuous intravenous (IV) fluid for 7 hours.
What is the total volume of IV fluid being infused, in liters?
Explanation
To answer this question, we need to calculate the infusion rate in mL per hour, then multiply it by the total time in hours, and finally divide it by 1000 to get the volume in litres.
The infusion rate in mL per hour is the amount of fluid that is given to a patient over a period of time. It can be calculated by dividing the total volume of fluid in mL by the total time in hours². In this case, the infusion rate is:
2.75 mL/min × 60 min/h = 165 mL/h
The total volume of fluid in mL is the infusion rate multiplied by the total time in hours. In this case, the total volume is:
165 mL/h × 7 h = 1155 mL
The volume in litres is the volume in mL divided by 1000. In this case, the volume in litres is:
1155 mL / 1000 = 1.16 L
Therefore, the correct answer is d. 1.16 L.
A primary healthcare provider prescribes 1.5 L of normal saline (NS) to be given over 24 hours for continuous intravenous (IV) infusion to a client who has diarrhea.
What should be the rate of infusion that is required to be set in the infusion pump?
Explanation
To calculate the rate of infusion, we need to divide the total volume to be infused (1.5 L) by the total time of infusion (24 hours)
1.5 L = 1500 mL (since 1 L = 1000 mL)
Dividing 1500 mL by 24 hours gives us the rate of 62.5 mL/hr.
A nurse needs to infuse esmolol to a patient weighing 65 kg. The dose on hand is 2,500 mg esmolol in 250 mL of fluid. The patient requires a dose of 200 mcg/kg/min to control a hypertensive crisis. Which rate should the nurse calculate to infuse this medication? Round to the nearest whole number.
Explanation
To calculate the infusion rate, we need to convert the patient's weight from kilograms to milligrams.
Patient's weight: 65 kg
Dose required: 200 mcg/kg/min
First, let's calculate the total dose required for the patient per minute: Dose required = 200 mcg/kg/min * 65 kg
= 13,000 mcg/min
Next, we need to convert the dose from micrograms to milligrams:
13,000 mcg/min = 13 mg/min
Now, let's determine the infusion rate. We have 2,500 mg of esmolol in 250 mL of fluid. Therefore, the concentration of esmolol in the fluid is:
Concentration = 2,500 mg / 250 mL
= 10 mg/mL
To find the infusion rate, we divide the dose required by the concentration: Infusion rate = 13 mg/min / 10 mg/mL
= 1.3 mL/mi
Since the options are in mL/hr, we need to convert the rate from mL/min to mL/hr:
1.3 mL/min * 60 min/hr = 78 mL/hr
Therefore, the correct answer is:
a. 78 mL/hr
A physician orders Dobutamine 10 mcg/kg/min for a patient. The patient is 110 lb. How many milligrams per hour should the patient receive?
Explanation
To calculate the dose in milligrams per hour, we need to convert the patient's weight from pounds to kilograms.
Patient's weight: 110 lb
To convert pounds to kilograms, we use the conversion factor: 1 lb = 0.4536 kg
Patient's weight in kilograms: 110 lb * 0.4536 kg/lb = 49.895 kg (rounded to 3 decimal places
The physician has ordered Dobutamine at a dose of 10 mcg/kg/min.
Dose required = 10 mcg/kg/min * 49.895 kg = 498.95 mcg/min
Next, we need to convert the dose from micrograms to milligrams.
498.95 mcg/min = 0.49895 mg/min
Finally, to determine the dose in milligrams per hour, we multiply the dose in milligrams per minute by 60 minutes to convert it to an hourly rate.
0.49895 mg/min * 60 min/hr = 29.937 mg/hr (rounded to 3 decimal places)
Therefore, the correct answer is:
a. 30 mg/hr
A nurse is preparing to administer 1 L of 0.9% sodium chloride solution to a client over 6 hours. The intravenous (IV) fluid has a drop factor of 15 gt/mL. What will be the gt/min flow rate?
Explanation
To calculate the gt/min flow rate, we need to determine the total number of drops and divide it by the total time in minutes.
First, let's convert the volume from liters to milliliters:
1 L = 1000 mL
Next, we need to determine the total number of drops. This can be calculated using the drop factor and the volume of the solution:
Total drops = Volume (mL) * Drop factor
= 1000 mL * 15 gt/mL
= 15000 gt
Now, we need to calculate the flow rate in gt/min. We divide the total drops by the total time in minutes: Flow rate = Total drops / Total time (min)
= 15000 gt / 360 min
≈ 41.67 gt/min (rounded to the nearest whole number)
Therefore, the correct answer is:
a. 41.6 gt/min
A healthcare provider orders nitroprusside (100 mg/1 mL) 3 mcg/kg/minute for a patient weighing 154 lb. What rate (mL/hr) should the nurse program into the IV pump?
Explanation
First, we need to convert the patient's weight from pounds to kilograms using the conversion factor 1 kg =
2.2 lb:
154 lb / 2.2 lb/kg = 70 kg
Next, we need to calculate the dose of nitroprusside in mcg/min using the formula Dose = Weight × Dosage:
Dose = 70 kg × 3 mcg/kg/min = 210 mcg/min
Then, we need to convert the dose of nitroprusside from mcg/min to mg/hr using the conversion factor 1 mg = 1000 mcg:
210 mcg/min × 1 mg/1000 mcg × 60 min/hr = 12.6 mg/hr
Finally, we need to calculate the rate of nitroprusside in mL/hr using the formula Rate = Dose/Concentration:
Rate = 12.6 mg/hr / 100 mg/mL = 0.126 mL/hr
To round to the nearest hundredth, we get 0.13 mL/hr, which is approximately equal to 1.26 mL/hr.
Therefore, the nurse should program the IV pump to deliver nitroprusside at a rate of 1.26 mL/hr.
A healthcare provider orders nitroprusside (100 mcg/1 mL) 3 mcg/kg/minute for a patient weighing 154 lb.
What rate (mL/hr) should the nurse program into the IV pump?
Explanation
To answer this question, we need to calculate the infusion rate in mL per hour by using the following formula²:
Infusion rate (mL/h) = Dose (mcg/kg/min) × Weight (kg) × 60 min/h × Volume (mL) / Concentration (mcg/mL)
In this case, the infusion rate is:
Infusion rate (mL/h) = 3 mcg/kg/min × 70 kg × 60 min/h × 250 mL / 2500 mg
We need to convert lb to kg by dividing by 2.2
Infusion rate (mL/h) = 3 mcg/kg/min × (154 lb / 2.2 kg/lb) × 60 min/h × 250 mL / 2500 mg
We need to convert mg to mcg by multiplying by 1000:
Infusion rte (mL/h) = 3 mcg/kg/min × (154 lb / 2.2 kg/lb) × 60 min/h × 250 mL / (2500 mg × 1000 mcg/mg)
We can simplify the equation by canceling out some units and numbers:
Infusion rate (mL/h) = 3 × 154 × 250 / (2.2 × 2500 × 1000)
We can use a calculator to get the final answer:
Infusion rate (mL/h) = 12.6363636363636 mL/h
Under which circumstance should a pediatric medication dose calculated from an adult dose be avoided?
Explanation
To answer this question, we need to understand the principles of pediatric dosage calculations and the factors that affect them. Pediatric dosages are usually calculated based on the child's weight or body surface area, and sometimes adjusted for age, organ function, or disease severity¹. However, not all medications that are used in adults are safe or effective in children. Some medications may have different pharmacokinetics, pharmacodynamics, adverse effects, or interactions in children than in adults².
Therefore, it is important to check the drug insert or label for any contraindications, warnings, or precautions for pediatric use before prescribing or administering a medication to a child. If the drug insert states that the medication is not for pediatric use, it means that the medication has not been tested or approved for use in children, or that it has been shown to be harmful or ineffective in children. In this case, a pediatric dose calculated from an adult dose should be avoided, as it may result in serious toxicity or therapeutic failure. The healthcare provider should consult a pediatric specialist, a pharmacist, or a reliable drug reference for alternative medications or dosing recommendations.
The other options are not correct because they do not necessarily warrant avoiding a pediatric dose calculated from an adult dose.
Option a. If the drug insert does not specify a pediatric dose, it means that there is insufficient data or evidence to support a specific pediatric dose, but it does not mean that the medication is contraindicated or unsafe in children. The healthcare provider should use clinical judgment and available resources to determine the appropriate dose for the child³.
Option b. If the child has an elevated temperature that has not responded to treatment, it means that the child may have an infection or inflammation that may affect the absorption, distribution, metabolism, or excretion of some medications. The healthcare provider should monitor the child's condition and adjust the dose accordingly, but it does not mean that the medication should be avoided altogether⁴.
Option c. If the child has gained or lost weight in the past month, it means that the child's weight may have changed significantly since the last dose calculation. The healthcare provider should weigh the child and recalculate the dose based on the current weight, but it does not mean that the medication should be avoided altogether.
A patient is receiving an IV of 500 mL of D5W (dextrose 5% in water).
How many grams (g) of dextrose are contained in this IV solution?
Explanation
Dextrose 5% in water (D5W) is an IV fluid that contains **5 grams of dextrose** per 100 mL of water². To calculate how many grams of dextrose are in 500 mL of D5W, you can use a simple proportion:
5 g / 100 mL = x g / 500 mL
Cross-multiply and solve for x:
x = (5 g * 500 mL) / 100 mL
x = 25 g
Therefore, there are **25 grams of dextrose** in 500 mL of D5W.
A primary healthcare provider prescribes 14 units of insulin to a client.
What should a nurse do while administering this medication to the client?
Explanation
Insulin is a hormone that helps regulate blood sugar levels. It is usually injected into the fat layer just under the skin (subcutaneous or SubQ) using a syringe and needle or a pen-like device². Insulin syringes are marked in units of insulin, not milliliters or cubic centimeters. The most common insulin syringe holds 1 mL of fluid and has markings for 100 units of insulin². A U-100 syringe means that for every 1 mL of fluid, there are 100 units of insulin³.
To administer 14 units of insulin, you would need to draw up 0.14 mL of fluid in a U-100 syringe. You would inject the insulin into your abdomen, upper arm, butocks, hip, or the front or side of the thigh¹. You would use a different area within the site each time you inject insulin to prevent lumps, swelling, or thickened skin¹.
The other options are incorrect because:
b) There is no need to divide the dose into two injections. This would increase the risk of infection and pain.
c) A tuberculin syringe is not designed for insulin administration. It is marked in milliliters or cubic centimeters, not units of insulin. Using a tuberculin syringe could result in an incorrect dose of insulin.
d) The timing of insulin administration depends on the type and duration of insulin. Some insulins are taken before meals, some are taken after meals, and some are taken once or twice a day. The primary healthcare provider should specify when to take the insulin.
A nurse will administer Zofran (ondansetron) 0.15 mg/kg over 15 minutes. The patient weighs 176 lb. The nurse receives the medication from the pharmacy mixed in 50 mL of normal saline.
How should the nurse set the IV pump to deliver the correct dose?
Explanation
To set the IV pump correctly, you need to calculate the following:
- The patient's weight in kilograms
- The dose of Zofran in milligrams
- The infusion rate in milliliters per hour
First, convert the patient's weight from pounds to kilograms by dividing by 2.2:
176 lb / 2.2 = 80 kg
Next, multiply the patient's weight by the dose of Zofran per kilogram to get the total dose in milligrams:
80 kg x 0.15 mg/kg = 12 mg
Then, use the formula for infusion rate to find how many milliliters per hour the IV pump should deliver:
Infusion rate (mL/h) = (Total volume (mL) x Flow factor (gt/mL)) / Time (min) x 60 min/h
Since the medication is mixed in 50 mL of normal saline and the infusion time is 15 minutes, plug in these values into the formula:
Infusion rate (mL/h) = (50 mL x 1 gt/mL) / 15 min x 60 min/h
Simplify and solve for the infusion rate:
Infusion rate (mL/h) = 200 mL/h
Nitroglycerin 125 mg diluted in 500 mL of D5W (dextrose 5% in water) is infusing at a rate of 42 mcg/minute for a patient with chest pain.
What rate (in mL/hr) should the nurse program into the IV pump to deliver this dose? Round your answer to the nearest tenth.
Explanation
To find the rate in mL/hr, you need to calculate the following:
- The concentration of nitroglycerin in the IV solution in mcg/mL
- The infusion rate in mL/hr using the formula: Infusion rate (mL/h) = (Dose (mcg/min) x 60 min/h) / Concentration (mcg/mL)
First, convert the concentration of nitroglycerin from mg to mcg by multiplying by 1000:
125 mg x 1000 = 125,000 mcg
Then, divide the amount of nitroglycerin by the volume of the IV solution to get the concentration in mcg/mL:
125,000 mcg / 500 mL = 250 mcg/mL
Next, plug in the values into the formula for infusion rate:
Infusion rate (mL/h) = (42 mcg/min x 60 min/h) / 250 mcg/mL
Simplify and solve for the infusion rate:
Infusion rate (mL/h) = 10.08 mL/h
Therefore, the nurse should program the IV pump to deliver **10.1 mL/h** to infuse nitroglycerin at 42 mcg/minute.
An order is received for Principen (ampicillin) 25 mg/kg IV for a toddler who weighs 22 lb. The dose is to be infused over 30 minutes. The ampicillin dose arrives from the pharmacy prepared in 50 mL of solution.
How many milliliters per hour should be administered?
Explanation
To find the milliliters per hour, you need to calculate the following:
- The patient's weight in kilograms
- The dose of Principen in milligrams
- The infusion rate in milliliters per hour using the formula: Infusion rate (mL/h) = (Total volume (mL) x Flow factor (gt/mL)) / Time (min) x 60 min/h
First, convert the patient's weight from pounds to kilograms by dividing by 2.2:
22 lb / 2.2 = 10 kg
Next, multiply the patient's weight by the dose of Principen per kilogram to get the total dose in milligrams:
10 kg x 25 mg/kg = 250 mg
Then, use the formula for infusion rate to find how many milliliters per hour the IV pump should deliver:
Infusion rate (mL/h) = (Total volume (mL) x Flow factor (gt/mL)) / Time (min) x 60 min/h
Since the medication is prepared in 50 mL of solution and the infusion time is 30 minutes, plug in these values into the formula:
Infusion rate (mL/h) = (50 mL x 1 gt/mL) / 30 min x 60 min/h
Simplify and solve for the infusion rate:
Infusion rate (mL/h) = 100 mL/h
Therefore, the nurse should administer **100 mL/h** to infuse Principen 250 mg over 30 minutes.
A patient is ordered 5 mg of IV Lopressor (metoprolol tartrate) to be administered over 60 seconds. The concentration is 1 mg/1 mL.
How many milliliters per minute should the nurse administer to the patient?
Explanation
To find the milliliters per minute, you need to calculate the following:
- The volume of Lopressor in milliliters
- The infusion rate in milliliters per minute using the formula: Infusion rate (mL/min) = Total volume (mL) / Time (min)
First, divide the dose of Lopressor by the concentration to get the volume in milliliters:
5 mg / 1 mg/mL = 5 mL
Next, use the formula for infusion rate to find how many milliliters per minute the IV pump should deliver:
Infusion rate (mL/min) = Total volume (mL) / Time (min)
Since the total volume is 5 mL and the time is 60 seconds or 1 minute, plug in these values into the formula:
Infusion rate (mL/min) = 5 mL / 1 min
Simplify and solve for the infusion rate:
Infusion rate (mL/min) = 5 mL/min
Therefore, the nurse should administer **5 mL/min** to infuse Lopressor 5 mg over 60 seconds.
A patient with deep vein thrombosis has heparin ordered. Heparin 25,000 units in 250 mL of D5W infuses at a rate of 12 mL/hr from 9:00 am to 11:00 am and 10 mL/hr from 11:00 am to 2:00 pm.
What is the total amount of heparin, in units, that the patient received from 9:00 am to 2:00 pm?
Explanation
To find the total amount of heparin, you need to calculate the following:
- The concentration of heparin in units per milliliter
- The volume of heparin infused from 9:00 am to 11:00 am and from 11:00 am to 2:00 pm
- The amount of heparin in units from each time period and the total amount
First, divide the amount of heparin by the volume of D5W to get the concentration in units per milliliter:
25,000 units / 250 mL = 100 units/mL
Next, multiply the infusion rate by the duration to get the volume infused in each time period:
From 9:00 am to 11:00 am (2 hours), the infusion rate is 12 mL/hr:
12 mL/hr x 2 hours = 24 mL
From 11:00 am to 2:00 pm (3 hours), the infusion rate is 10 mL/hr:
10 mL/hr x 3 hours = 30 mL
Then, multiply the volume infused by the concentration to get the amount of heparin in units in each time period:
From 9:00 am to 11:00 am, the volume infused is 24 mL:
24 mL x 100 units/mL = 2400 units
From 11:00 am to 2:00 pm, the volume infused is 30 mL:
30 mL x 100 units/mL = 3000 units
Finally, add the amounts of heparin from each time period to get the total amount:
2400 units + 3000 units = 5400 units
Therefore, the patient received **5400 units** of heparin from 9:00 am to 2:00 pm.
A patient is ordered 5 mg of IV Lopressor (metoprolol tartrate) to be administered over 2 minutes. The concentration is 1 mg/1 mL.
How many milligrams per minute should the patient receive?
Explanation
To find the milligrams per minute, you need to calculate the following:
- The volume of Lopressor in milliliters
- The infusion rate in milliliters per minute using the formula: Infusion rate (mL/min) = Total volume (mL) / Time (min)
- The dose of Lopressor in milligrams per minute using the formula: Dose (mg/min) = Infusion rate (mL/min) x Concentration (mg/mL)
First, divide the dose of Lopressor by the concentration to get the volume in milliliters:
5 mg / 1 mg/mL = 5 mL
Next, use the formula for infusion rate to find how many milliliters per minute the IV pump should deliver:
Infusion rate (mL/min) = Total volume (mL) / Time (min)
Since the total volume is 5 mL and the time is 2 minutes, plug in these values into the formula:
Infusion rate (mL/min) = 5 mL / 2 min
Simplify and solve for the infusion rate:
Infusion rate (mL/min) = 2.5 mL/min
Then, use the formula for dose to find how many milligrams per minute the patient should receive:
Dose (mg/min) = Infusion rate (mL/min) x Concentration (mg/mL)
Since the infusion rate is 2.5 mL/min and the concentration is 1 mg/mL, plug in these values into the formula:
Dose (mg/min) = 2.5 mL/min x 1 mg/mL
Simplify and solve for the dose:
Dose (mg/min) = 2.5 mg/min
Therefore, the patient should receive **2.5 mg/min** of Lopressor.
After assessing a client, a primary healthcare provider prescribes diphenhydramine 25 mg IV STAT for anaphylaxis. The pharmacy supplies a vial with a concentration of 50 mg/mL.
How much and when should a nurse administer this medication?
Explanation
To find how much medication to administer, you need to calculate the following:
- The volume of diphenhydramine in milliliters
- The infusion time in minutes
First, divide the dose of diphenhydramine by the concentration to get the volume in milliliters:
25 mg / 50 mg/mL = 0.5 mL diphenhydramine should be diluted in 10 to 20 mL of normal saline and infused over at least 2 minutes.
Therefore, the nurse should administer **0.5 mL** of diphenhydramine diluted in 10 to 20 mL of normal saline over **at least 2 minutes**.
The nurse should administer this medication **as soon as possible** after receiving the order and the medication from the pharmacy, as STAT means immediately or urgently. The nurse should also monitor the client for signs of improvement or adverse reactions.
What is the correct angle for giving an intradermal injection?
Explanation
The correct angle for giving an intradermal injection is **10 to 15 degrees**. This angle allows the needle to enter the dermis, which is the layer of skin just below the epidermis. The needle should be inserted almost flat against the patient's skin, with the bevel side up. A small blister or bleb should form under the skin after injecting the medication.

A client is receiving an intravenous infusion of 1.5 L of saline solution at a rate of 75 mL/hr.
How many hours will it take to finish the infusion at the current rate?
Explanation
To find the hours to finish the infusion, you need to calculate the following:
- The volume of saline solution in milliliters
- The time in hours using the formula: Time (h) = Total volume (mL) / Infusion rate (mL/h)
First, convert the volume of saline solution from liters to milliliters by multiplying by 1000:
1.5 L x 1000 = 1500 mL
Next, use the formula for time to find how many hours it will take to infuse the saline solution at the current rate:
Time (h) = Total volume (mL) / Infusion rate (mL/h)
Since the total volume is 1500 mL and the infusion rate is 75 mL/h, plug in these values into the formula:
Time (h) = 1500 mL / 75 mL/h
Simplify and solve for the time:
Time (h) = 20 h
Therefore, it will take **20 hours** to finish the infusion at the current rate.
The patient needs both regular insulin and NPH insulin to be administered subcutaneously. The nurse will mix both insulins in the same syringe.
What is the correct technique for preparing this insulin order?
Explanation
The correct technique for preparing this insulin order is to follow these steps¹²:
- Perform hand hygiene and put on gloves.
- Mix NPH (cloudy) insulin by gently rotating the vial between the palms of your hands. Do not shake the vial.
- Clean the tops of both vials with alcohol swabs and let them dry.
- Draw up the amount of air equal to the dose of NPH insulin into a syringe. Inject the air into the NPH vial without touching the needle to the solution. Withdraw the needle and syringe without drawing up any insulin. This will create positive pressure in the NPH vial and make it easier to draw up later.
- Draw up the amount of air equal to the dose of regular (clear) insulin into the same syringe. Inject the air into the regular vial and invert the vial. Make sure the needle tip is below the fluid level and draw up slightly more than the dose of regular insulin. Tap the syringe gently to remove any air bubbles and push out any excess insulin to get the exact dose. Withdraw the needle and syringe from the regular vial.
- Reinsert the needle and syringe into the NPH vial without touching the needle to the solution. Invert the vial and draw up slightly more than the dose of NPH insulin. Tap the syringe gently to remove any air bubbles and push out any excess insulin to get the exact dose. Withdraw the needle and syringe from the NPH vial.
- Check that you have the correct doses of both insulins in one syringe. The total volume should be equal to the sum of both doses.
- Administer the dose within 5 to 10 minutes after drawing up because regular insulin binds to NPH and this decreases its action.

Sign Up or Login to view all the 69 Questions on this Exam
Join over 100,000+ nursing students using Nursingprepexams’s science-backend flashcards, practice tests and expert solutions to improve their grades and reach their goals.
Sign Up Now

